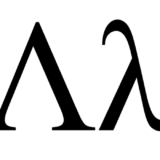Lambda Calculus Notes
The following are my brief notes on the basic of Lambda Calculus. They are primarily just a public posting of my personal notes, and are not meant to be a tutorial per-se. Though it is my hope that someone else besides me would find them to be of use. All of the sources I used to compile these notes are including in the bottom of the page.
Lambda Syntax
Expression (Mention) E ::= X Function (Application) | ?x.E -- ? and . are the only keywords in the lambda calculus Application (Application) | E E
An expression can be surrounded with parenthesis for clarity.
(E) ::= E
Function Application (Left Association)
E1E2E3...En => (...((E1E2)E3)...En) ^ n-4 more close parens, hence the use of ...
Functions (or Lambda Abstractions)
An function (or abstraction) is another name for an anonymous function. In the lambda calculus an abstraction has two parts, a head that contains a single parameter and ends before a period, and a body that contains an expression.
?? . ? ?? . ? ?? . ? ^^ ^ ^ Is the head Bound the head Is the body (tail)
Function Argument
A function argument is declared in the header, and must be immediately preceded by a ? .
??.? ^ Is a function argument.
Bound Variables
A bound variable is a variable in the function body that has the same identifier as the function argument.
??.? ^ Is a bound variable
A variable x (x can have any name y, z, etc.) is bound if one of the two following cases holds:
- If the x = x1 or x is bound to E, then x is bound in λ x1.E
- If x is bound to E1 or E2, then x is bound in E1 E2
- In this case “x is bound” means “there is an x bound”.
Free Variables
??.?a ^ Is a free variable (??.?)(?y.yx) ^ ^ Bound Free -- Note: The x in the first expression isn't the same as the x in the second.
A variable x (x can have an name y, z, etc.) is free in an expression (E) if one of the three following cases holds:
- If the free variables of x is x, then x is free
- x !=x1 and x is free in E then x is free in (λ x1.E)
- If x is free in E1 or E2 in, then x is free
- In this case “x is free” means “there is an x free”.
Function Application
(?x.x)y -- The identity function applied to y. The parenthesis avoid ambiguity. y
Substitution Shorthand
The two common notations used to express the substitution process that occurs during function application.this is [y/x] and [x:=y] which
[y/x]E
The above can be read as, y will replace all occurrences of x in the expression E.
(?x.xa)y = [y/x]xa = ya
[x:= E]
The above can be read as, all occurrences of x will be replaced with E.
(?x.xa)y [x:=y] ya
Applying Substitutions
(??.E1)E2
Example 1
(??.(?t.xt))y ^ ^ (??.(E1)) E2 -- x in E1 is free, but bound by ?? in the function head, so it will be replaced with y. ?t.yt
In order to perform this substitution it is important to remember that the variables in function bodies can only be substitutes during application if they are bound only to that function. That is, if a function contains a function in its body, and the body function has a variable bound to it with the same name as the outer function, then an outer substitution must not change the inner functions variable.
(?x.x)(?y.y)z -- The second function is applied to the first (?y.y)z -- z is applied to the function z
Example 3
(????.??(??))(???.?)(??.?) (??.??.??.??(??))(?m.?n.m)(?p.p) -- Function arguments are expanded to include the lambdas that bind them ^ ^ E1 E2 -- E1 = (??.??.??.??(??)) is then applied to E2 = (?m.?n.m) -- [?m.?n.m / x] ??.??.??(??) = ??.??.(?m.?n.m)?(??) (??.??.(?m.?n.m)?(??))(?p.p) ^ ^ E1 E2 -- E1 = (?m.?n.m) is then applied to E2 = z. -- [z / m] ?n.m = ?n.z = z (??.??.?)(?p.p) ^ ^ E1 E2 -- E1 = (??.??.?) is then applied to E2 = (?p.p) -- [?p.p / y] ??.? = ??.? ??.?
Sources
- A Tutorial Introduction to the Lambda Calculus
- Haskell Programming from First Principles
- Haskell Wiki