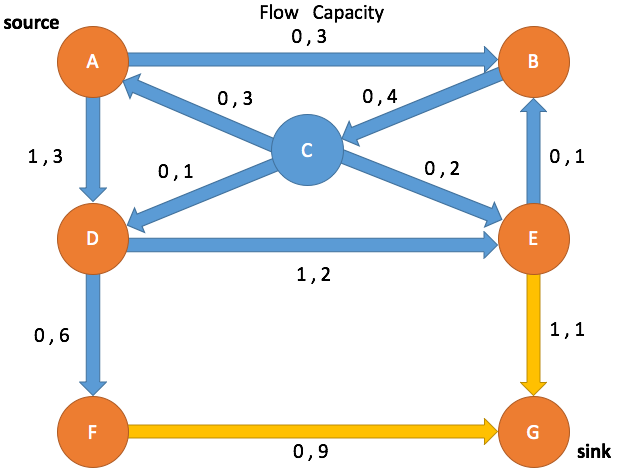
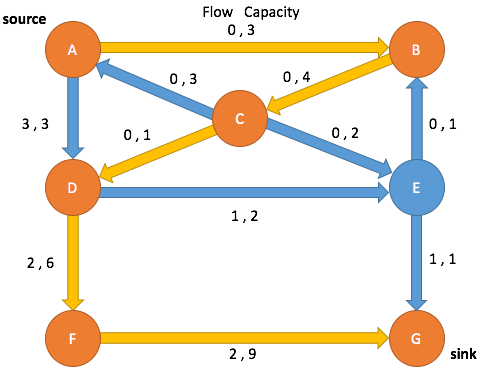
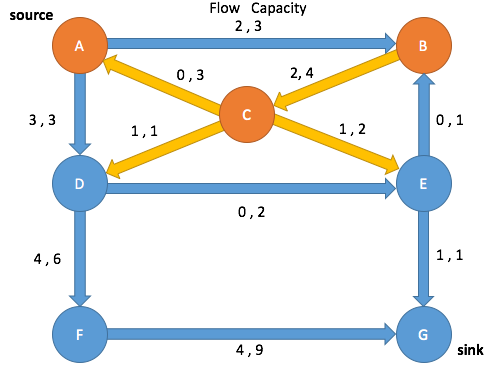
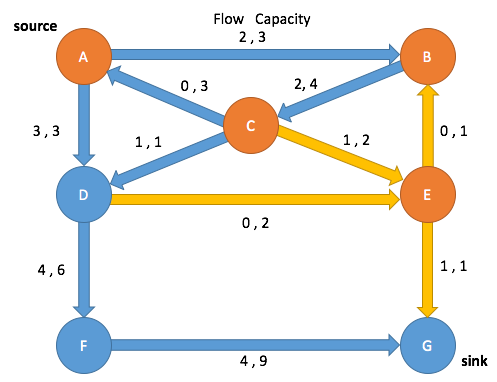
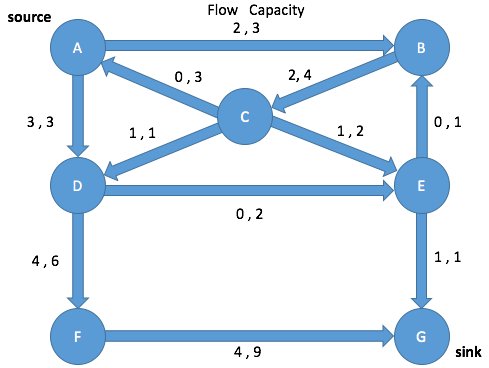
Ford-Fulkerson Max Flow Algorithm
In this post I will step through the execution of the Ford-Fulkerson Max Flow algorithm using the Edmond-Karp Breadth First Search method. If you are learning this for the first time I suggest you watch this video tutorial, in which the same graph is used, and look at this Java source code for more implementation details.
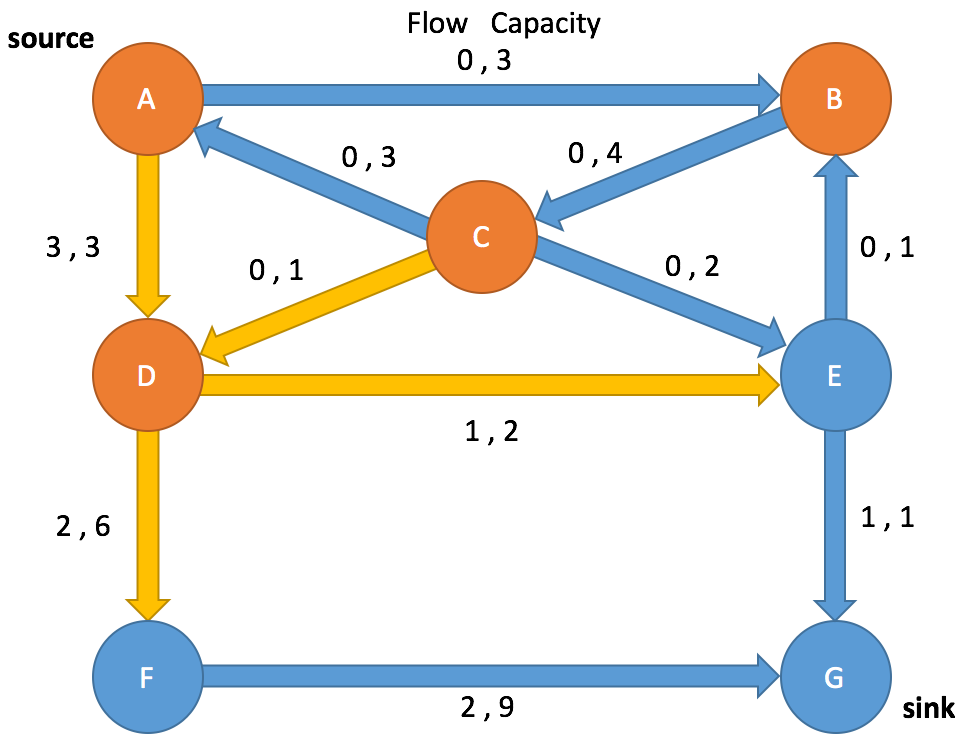
Residual Graph
Ford-Fulkerson Algorithm
Start with a flow of 0.
While there exists and augmenting path:
- Find an augmenting path
- Compute the bottleneck capacity
- Increase flow on that path by the bottleneck capacity
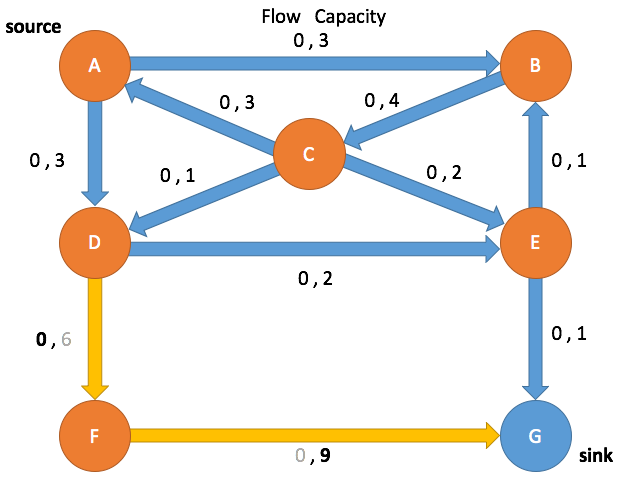
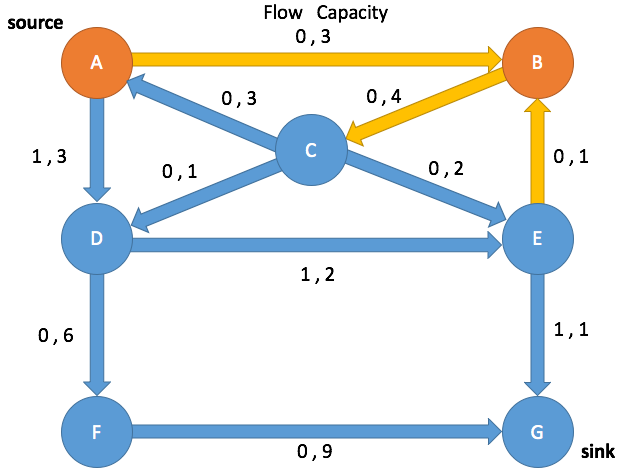
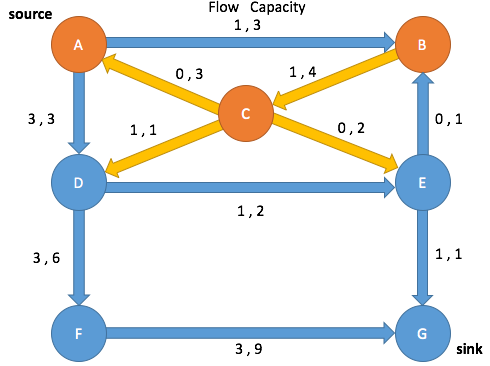
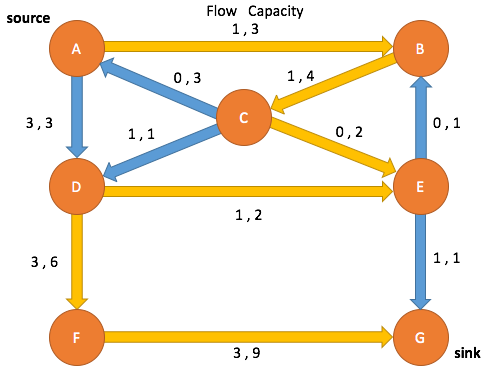
Path Search: Iteration 1
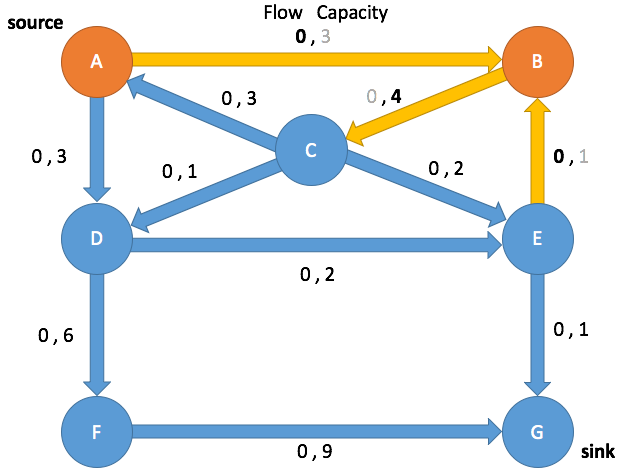
Enqueue A and mark as visited
|
A
|
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 0, 3) (C→A, 0, 0)
|
|
–
|
B |
–
|
–
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
–
|
C |
–
|
–
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
|
–
|
D |
–
|
–
|
(A→D, 0, 3) (C→D, 0, 1) (D→E, 0, 2) (D→F, 0, 6)
|
|
–
|
E |
–
|
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 0, 2) (E→G, 0, 1)
|
|
–
|
F |
–
|
–
|
(D→F, 0, 6) (F→G, 0, 9)
|
|
–
|
G |
–
|
–
|
(F→G, 0, 9) (E→G, 0, 1)
|
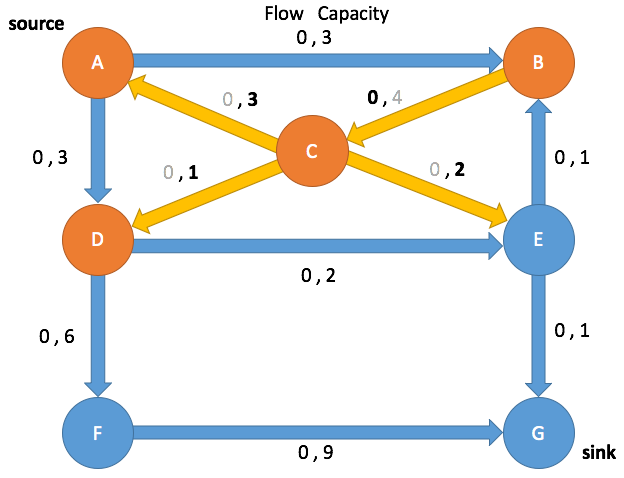
Dequeue A
|
A
|
Find edges incident to A with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
A
|
B
|
False
|
3 – 0 = 3
|
True
|
|
A→D
|
A
|
D
|
False
|
3 – 0 = 3
|
True
|
|
C→A
|
A
|
C
|
False
|
0 |
False
|
residualCapacity(Vertex to) {
if (to != edge.to()) {
return edge.flow;
}
else {
return edge.capacity - edge.flow;
}
Mark vertices B and D as visited, add them to the queue, and add A as their parent, and add the edges to B and D.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To
|
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A |
True
|
(A→B, 0, 3) (A→D, 0, 3) (C→A, 0, 0)
|
|
|
A
|
B
|
True
|
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
–
|
C |
–
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
|
| A |
D
|
True
|
(A→D, 0, 3)
|
(A→D, 0, 3) (C→D, 0, 1) (D→E, 0, 2) (D→F, 0, 6)
|
|
–
|
E |
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 0, 2) (E→G, 0, 1)
|
|
|
–
|
F |
–
|
(D→F, 0, 6) (F→G, 0, 9)
|
|
|
–
|
G |
–
|
(F→G, 0, 9) (E→G, 0, 1)
|
Dequeue B
|
B
|
D
|
Find edges incident to B with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
B |
A
|
True
|
0 |
False
|
|
B→C
|
B
|
C
|
False
|
4 – 0 = 4
|
True
|
|
E→B
|
B
|
E
|
False
|
0 |
False
|
Mark vertices C as visited, add it to the queue, set B as its parent, and add the edge to C.
Data Structures
| Parent | To |
Visited
|
Edge To
|
Adjacent Edges (Edge, Flow, Capacity)
|
| – | A |
True
|
(A→B, 0, 3) (A→D, 0, 3) (C→A, 0, 0)
|
|
|
A
|
B |
True
|
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| B | C |
True
|
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| A | D |
True
|
(A→D, 0, 3)
|
(A→D, 0, 3) (C→D, 0, 1) (D→E, 0, 2) (D→F, 0, 6)
|
| – |
E
|
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 0, 2) (E→G, 0, 1)
|
|
| – | F |
–
|
(D→F, 0, 6) (F→G, 0, 9)
|
|
| – | G |
–
|
(F→G, 0, 9) (E→G, 0, 1)
|
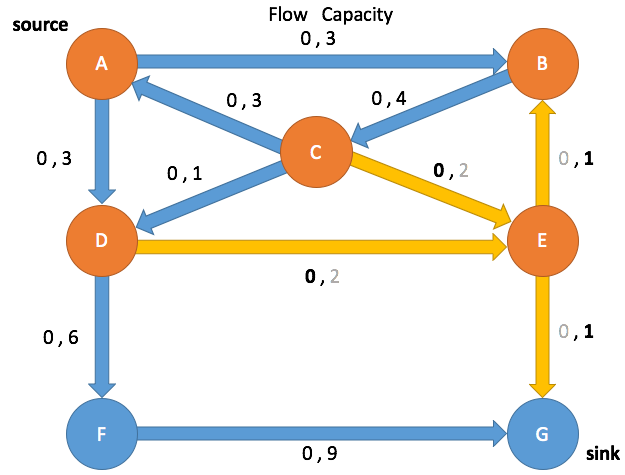
Dequeue D
|
D
|
C
|
Find edges incident to D with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→D
|
D
|
A
|
True
|
0 |
False
|
|
C→D
|
D
|
C
|
True
|
0 |
False
|
|
D→E
|
D
|
E
|
False
|
2
|
True
|
|
D→F
|
D
|
F
|
False
|
6
|
True
|
Mark vertices E and F as visited, add them to the Queue, set their parent to D, and add the edges.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To
|
Adjacent Edges (Edge, Flow, Capacity)
|
| – | A |
True
|
(A→B, 0, 3) (A→D, 0, 3) (C→A, 0, 0)
|
|
| A | B |
True
|
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
B
|
C |
True
|
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| A | D |
True
|
(A→D, 0, 3)
|
(A→D, 0, 3) (C→D, 0, 1) (D→E, 0, 2) (D→F, 0, 6)
|
|
D
|
E |
True
|
(D→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 0, 2) (E→G, 0, 1)
|
|
D
|
F |
True
|
(D→F, 0, 6)
|
(D→F, 0, 6) (F→G, 0, 9)
|
| – | G |
–
|
(F→G, 0, 9) (E→G, 0, 1)
|
Dequeue C
|
C
|
E
|
F
|
Find edges incident to C with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
C→A
|
C
|
A
|
True
|
3 |
False
|
|
B→C
|
C
|
B
|
True
|
0 |
False
|
|
C→D
|
C
|
D
|
True
|
1
|
False
|
|
C→E
|
C
|
E
|
True
|
2
|
False
|
Nothing to add since all adjacent vertices have been visited.
Dequeue E
|
E
|
F
|
Find edges incident to E with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→B
|
E
|
B |
True
|
1 |
False
|
|
C→E
|
E
|
C |
True
|
0 |
False
|
|
D→E
|
E
|
D
|
True
|
2 |
False
|
|
E→G
|
E
|
G
|
False
|
1 |
True
|
Mark vertices G as visited, add them to the Queue, and set their parent to G.
Data Structures
| Parent | To |
Visited
|
Edge To
|
Adjacent Edges (Edge, Flow, Capacity)
|
| – | A |
True
|
(A→B, 0, 3) (A→D, 0, 3) (C→A, 0, 0)
|
|
| A | B |
True
|
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| B | C |
True
|
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| A | D |
True
|
(A→D, 0, 3)
|
(A→D, 0, 3) (C→D, 0, 1) (D→E, 0, 2) (D→F, 0, 6)
|
| D | E |
True
|
(D→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 0, 2) (E→G, 0, 1)
|
| D | F |
True
|
(D→F, 0, 6)
|
(D→F, 0, 6) (F→G, 0, 9)
|
| E | G | True |
(E→G, 0, 1)
|
(F→G, 0, 9) (E→G, 0, 1)
|
Dequeue F
|
F
|
G
|
Find edges incident to F with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
D→F
|
F
|
D
|
True
|
0 |
False
|
|
F→G
|
F
|
G
|
True | 9 | False |
Nothing to add since all adjacent vertices have been visited.
Dequeue G
|
G
|
Find edges incident to G with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→G
|
G |
E
|
True
|
0 |
False
|
|
F→G
|
G
|
F
|
True
|
9 |
False
|
Nothing to add.
HALT: Queue Empty
Determining the Path
We can work backwards from the sink in order to determine the path. G, E, D, A (A→D→E→G).
Determining the Bottleneck Capacity
Starting from the sink vertex G we work backwards to the source calculating the min residual capacity.
bottleneck = Infinity;
v = Graph.sink();
while (v != Graph.source()) {
residualCapacity = edgeTo(v).residualCapacity();
bottleneck = Math.min(edgeTo(v).residualCapacity(), bottleneck);
v = parent(v);
}
| Parent | To |
Back Edge
|
Capacity | Flow |
Max Flow
|
Bottleneck (min flow) |
New Flow
|
Edge To Before
|
Edge To After
|
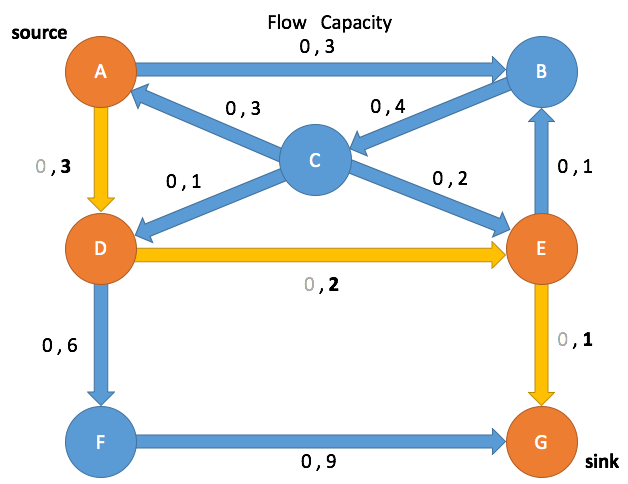
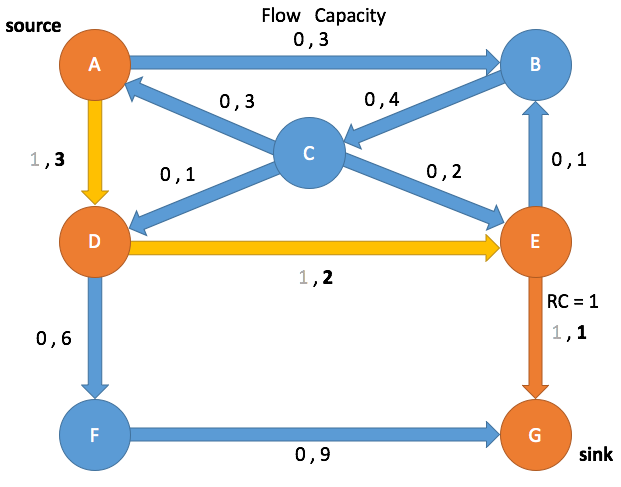
| A | D |
False
|
3 |
0
|
3 – 0 = 3
|
1
|
1
|
(A→D, 0, 3)
|
(A→D, 1, 3)
|
| D | E |
False
|
2 |
0
|
2 – 0 = 2
|
1
|
1
|
(D→E, 0, 2)
|
( (D→E, 1, 2)
|
| E | G |
False
|
1 |
0
|
1-0 = 1
|
1
|
1
|
(E→G, 0, 1)
|
(E→G, 1, 1)
|
Edge E→G: bottleneck = 1
Updating (Augmenting) the Path Edges
To augment the path we work backwards as we did when determining the bottleneck capacity, but this time we update the residual capacity of the edge reverence in edgeTo for each vertex on the path.
v = G.sink();
while (v != G.source()) {
edgeTo[v].addFlow(v, bottleneck);
v = parent[v];
}
Edge {
...
addFlow(toVertex, value) {
if (toVertex == from) {
flow = flow - value;
}
else {
flow = flow + value;
}
}
}
| Parent | To |
Path Bottleneck
|
Edge To Before
|
Edge To After
|
| A | D |
1
|
(A→D, 0, 3)
|
(A→D, 1, 3)
|
| D | E |
1
|
(D→E, 0, 2)
|
( (D→E, 1, 2)
|
| E | G |
1
|
(E→G, 0, 1)
|
(E→G, 1, 1)
|
Critical Edge = E→G
Max Flow = 1
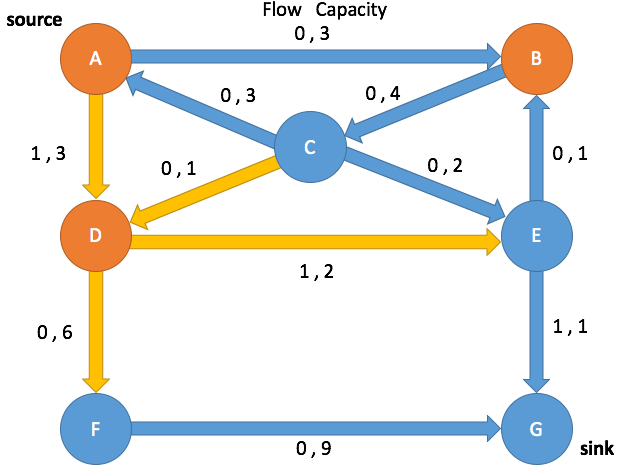
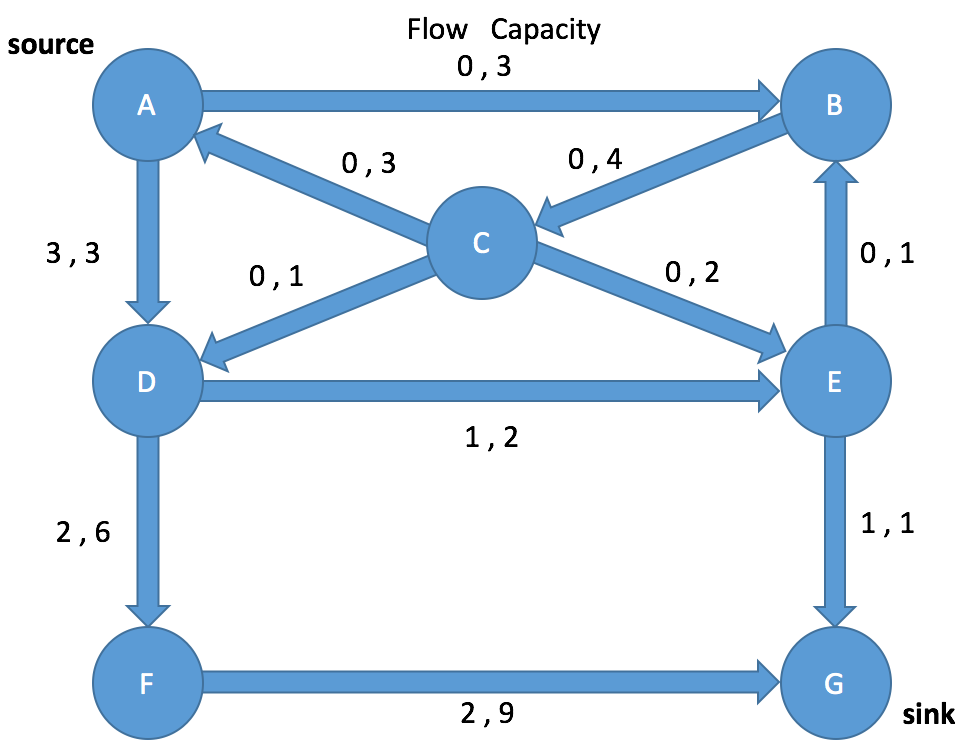
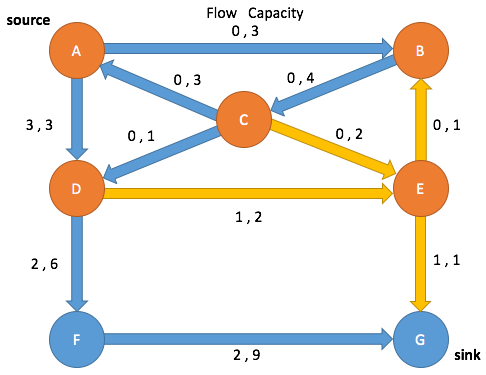
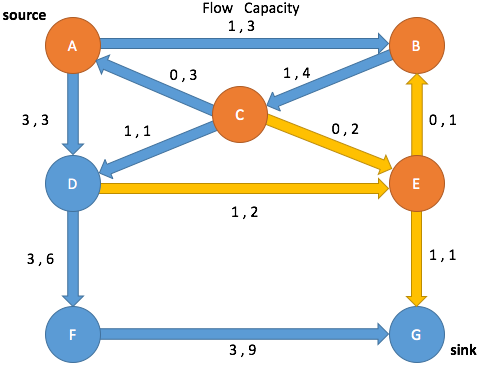
Path Search: Iteration 2
Enqueue A and mark as visited
|
A
|
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 1, 3) (C→A, 0, 0)
|
|
–
|
B |
–
|
–
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
–
|
C |
–
|
–
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
|
–
|
D |
–
|
–
|
(A→D, 0, 1) (C→D, 0, 1) (D→E, 01, 2) (D→F, 0, 6)
|
|
–
|
E |
–
|
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
|
–
|
F |
–
|
–
|
(D→F, 0, 6) (F→G, 0, 9)
|
|
–
|
G |
–
|
–
|
(F→G, 0, 9) (E→G, 1, 1)
|
Dequeue A
|
A
|
Find edges incident to A with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
A
|
B
|
False
|
3 |
True
|
|
A→D
|
A
|
D
|
False
|
3 – 1 = 2
|
True
|
|
C→A
|
A
|
C
|
False
|
0 | False |
Mark vertices B and D as visited, add them to the queue, and add A as their parent, and add the edges to B and D.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 1, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
–
|
C |
–
|
–
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| A | D |
True
|
(A→D, 1, 3)
|
(A→D, 0, 1) (C→D, 0, 1) (D→E, 01, 2) (D→F, 0, 6)
|
|
–
|
E |
–
|
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
|
–
|
F |
–
|
–
|
(D→F, 0, 6) (F→G, 0, 9)
|
|
–
|
G |
–
|
–
|
(F→G, 0, 9) (E→G, 1, 1)
|
Dequeue B
|
B
|
D
|
Find edges incident to B with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
B |
A
|
True
|
0 |
False
|
|
B→C
|
B
|
C
|
False
|
4
|
True
|
|
E→B
|
B
|
E
|
False
|
0 |
False
|
Mark vertices C as visited, add it to the queue, set B as its parent, and add the edge to C.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 1, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
B
|
C | True |
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| A | D |
True
|
(A→D, 1, 3)
|
(A→D, 0, 1) (C→D, 0, 1) (D→E, 01, 2) (D→F, 0, 6)
|
|
–
|
E |
–
|
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
|
–
|
F |
–
|
–
|
(D→F, 0, 6) (F→G, 0, 9)
|
|
–
|
G |
–
|
–
|
(F→G, 0, 9) (E→G, 1, 1)
|
Dequeue D
|
D
|
C
|
Find edges incident to D with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→D
|
D
|
A
|
True
|
1 |
False
|
|
C→D
|
D
|
C
|
True
|
0 |
False
|
|
D→E
|
D
|
E
|
False
|
1 |
True
|
|
D→F
|
D
|
F
|
False
|
6
|
True
|
Mark vertices E and F as visited, add them to the Queue, set their parent to D, and add the edges.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 1, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
B
|
C | True |
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| A | D |
True
|
(A→D, 1, 3)
|
(A→D, 0, 1) (C→D, 0, 1) (D→E, 01, 2) (D→F, 0, 6)
|
|
D
|
E | True |
(D→E, 01, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
|
D
|
F | True |
(D→F, 0, 6)
|
(D→F, 0, 6) (F→G, 0, 9)
|
|
–
|
G |
–
|
–
|
(F→G, 0, 9) (E→G, 1, 1)
|
Dequeue C
|
C
|
E
|
F
|
Find edges incident to C with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
C→A
|
C
|
A
|
True
|
3
|
False
|
|
B→C
|
C
|
B
|
True
|
0 |
False
|
|
C→D
|
C
|
D
|
True
|
2 |
False
|
|
C→E
|
C
|
E
|
True
|
2 |
False
|
Nothing to add since all adjacent vertices have been visited.
Dequeue E
|
E
|
F
|
Find edges incident to E with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→B
|
E
|
B |
True
|
1 |
False
|
|
C→E
|
E
|
C |
True
|
0 |
False
|
|
D→E
|
E
|
D
|
True
|
1 |
False
|
|
E→G
|
E
|
G
|
False
|
0 |
False
|
Nothing to add since all adjacent vertices have been visited.
Dequeue F
|
F
|
Find edges incident to F with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
D→F
|
F
|
D
|
True
|
0 |
False
|
|
F→G
|
F
|
G
|
False | 9 | True |
Mark vertices G as visited, add it to the Queue, set their parent to F, and add the edges.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 1, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
|
B
|
C | True |
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| A | D |
True
|
(A→D, 1, 3)
|
(A→D, 0, 1) (C→D, 0, 1) (D→E, 01, 2) (D→F, 0, 6)
|
|
D
|
E | True |
(D→E, 01, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
|
D
|
F | True |
(D→F, 0, 6)
|
(D→F, 0, 6) (F→G, 0, 9)
|
| F | G | True |
(F→G, 0, 9)
|
(F→G, 0, 9) (E→G, 1, 1)
|
Dequeue G
| G |
Find edges incident to F with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→G
|
G
|
E
|
True
|
1 |
False
|
|
F→G
|
G |
F
|
True
|
0 |
False
|
Nothing to add.
HALT: Queue Empty
Determining the Path
Working backwards from G using the edgeTo array we determine the path to be A, D, F, G.
Determining the Bottleneck Capacity
Starting from the sink vertex G we work backwards to the source calculating the min residual capacity. The bottleneck is determined to be at edge
| Parent | To |
Back Edge
|
Capacity | Flow |
Max Flow
|
Bottleneck (min flow) |
New Flow
|
Edge To Before
|
Edge To After
|
| A | D |
False
|
3 | 1 |
2
|
2 | 3 |
(A→D, 1, 3)
|
(A→D, 3, 3)
|
| D | F |
False
|
6 | 0 |
6
|
2 | 2 |
(D→F, 0, 6)
|
( (D→F, 2, 6)
|
| F | G |
False
|
9 |
0
|
9 | 2 | 2 |
(F→G, 0, 9)
|
(F→G, 2, 9)
|
Updating (Augmenting) the Path Edges
To augment the path we work backwards as we did when determining the bottleneck capacity, but this time we update the residual capacity of the edge reverence in edgeTo for each vertex on the path.
| Parent | To |
Path Bottleneck
|
Edge To Before
|
Edge To After
|
| A | D | 2 |
(A→D, 1, 3)
|
(A→D, 3, 3)
|
| D | F | 2 |
(D→F, 0, 6)
|
(D→F, 2, 6)
|
| F | G | 2 |
(F→G, 0, 9)
|
(F→G, 2, 9)
|
Critical Edge = A→D
Max Flow = 1 + 2 = 3
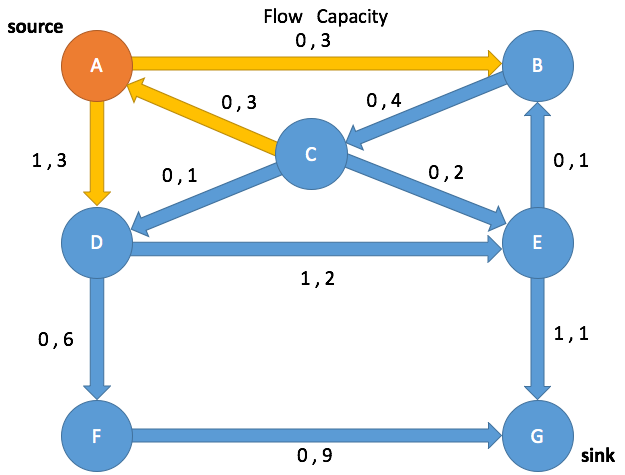
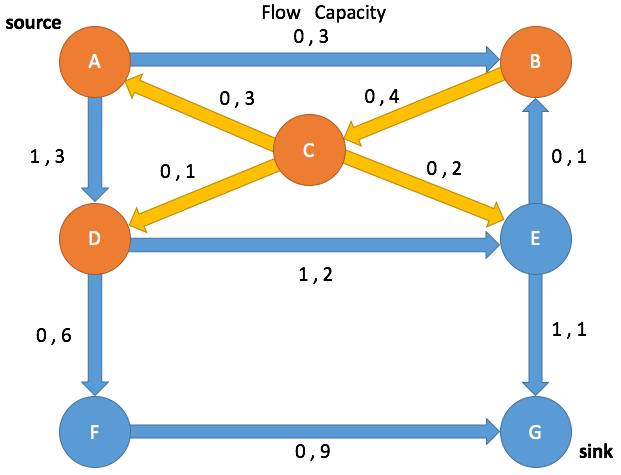
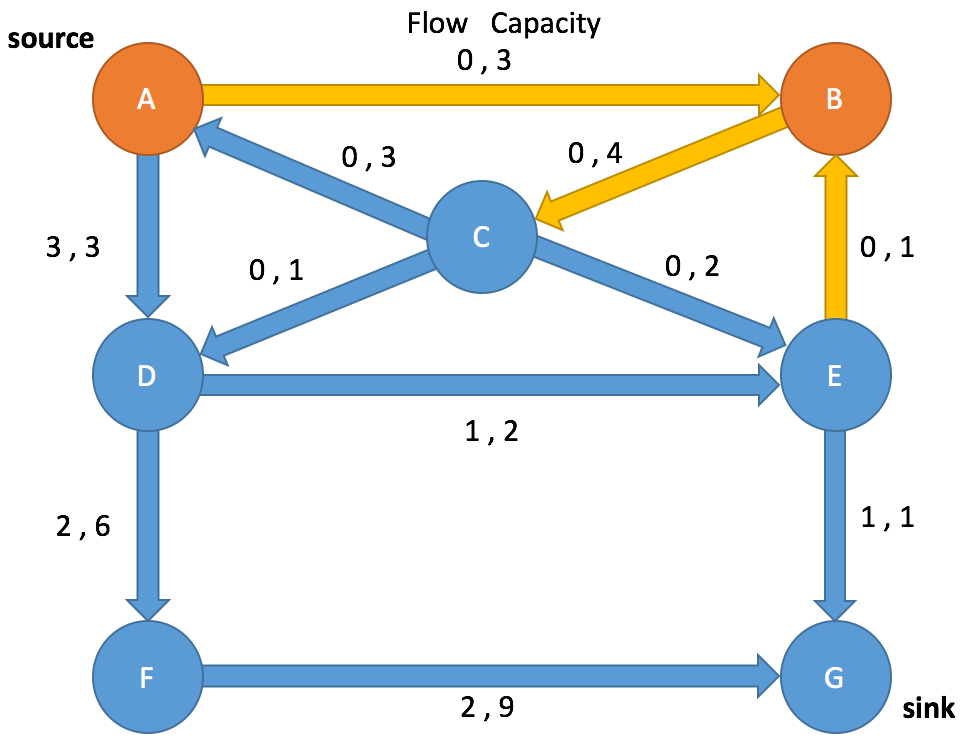
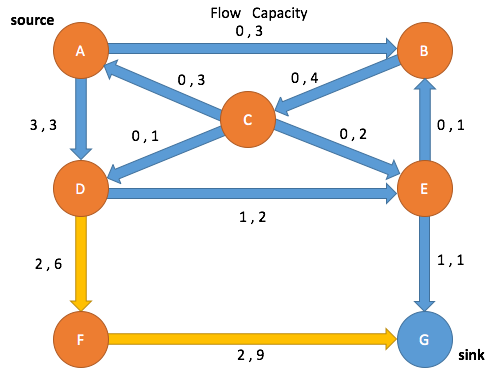
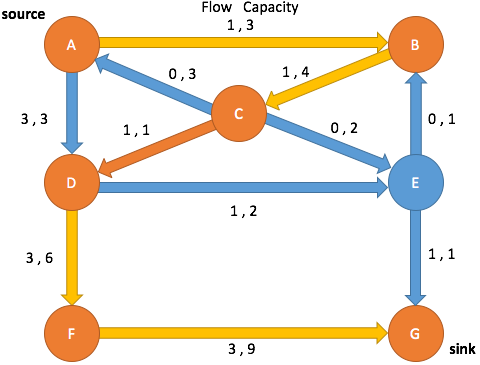
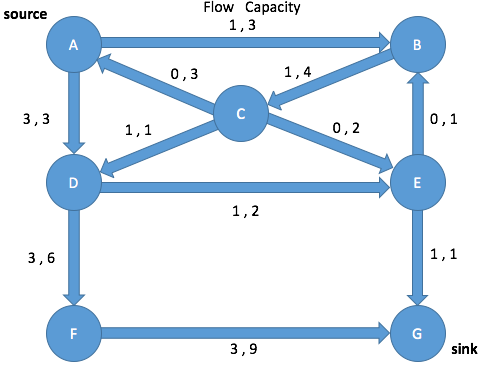
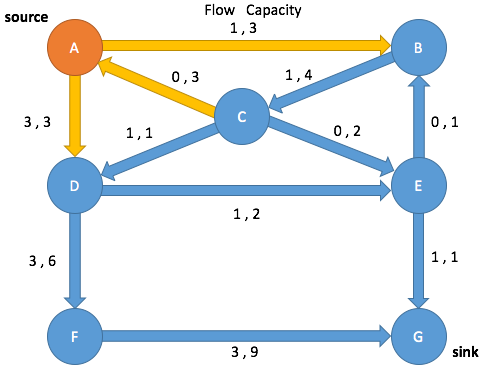
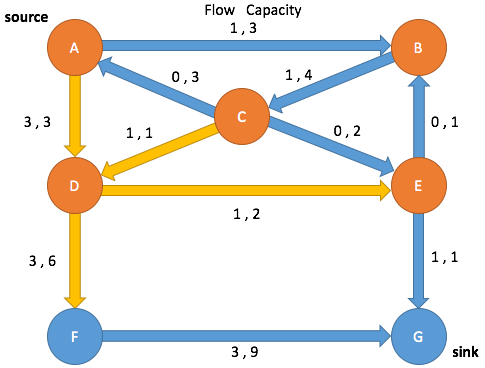
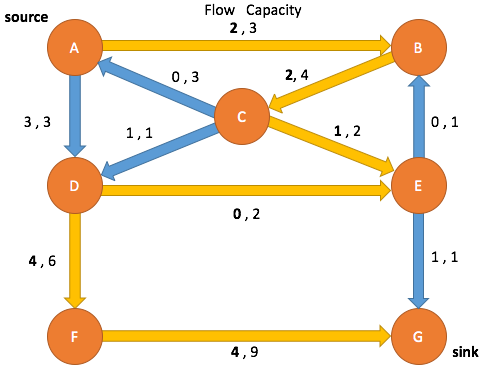
Path Search: Iteration 3
Enqueue A and mark as visited
|
A
|
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0 3) (A→D, 3, 3) (C→A, 0, 0)
|
| – | B | – |
–
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| – | C | – |
–
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| – | D |
–
|
–
|
(A→D, 3, 3) (C→D, 0, 1) (D→E, 01, 2) (D→F, 2, 6)
|
| – | E | – |
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 2, 6) (F→G, 2, 9)
|
| – | G | – |
–
|
(F→G, 2, 9) (E→G, 1, 1)
|
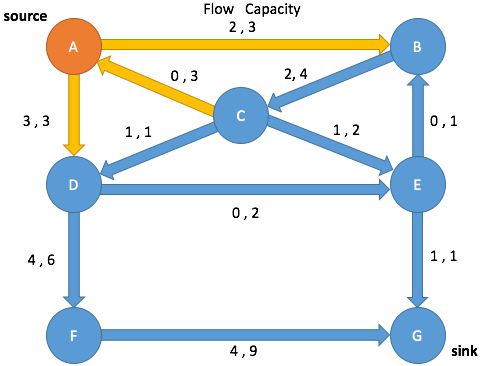
Dequeue A
|
A
|
Find edges incident to A with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
A
|
B
|
False
|
3
|
True
|
|
A→D
|
A
|
D
|
False
|
0 | False |
|
C→A
|
A
|
C
|
False
|
0 | False |
Mark vertices B as visited, add them to the queue, and add A as their parent, and add the edge to B.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| – | C | – |
–
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| – | D |
–
|
–
|
(A→D, 3, 3) (C→D, 0, 1) (D→E, 01, 2) (D→F, 2, 6)
|
| – | E | – |
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 2, 6) (F→G, 2, 9)
|
| – | G | – |
–
|
(F→G, 2, 9) (E→G, 1, 1)
|
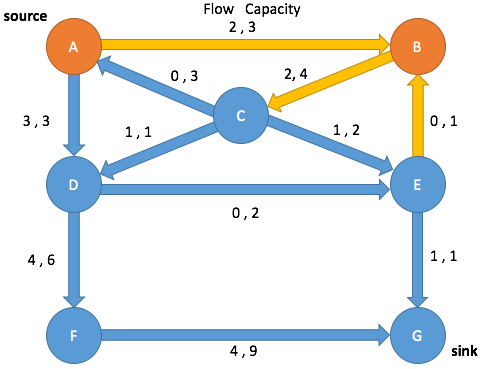
Dequeue B
|
B
|
Find edges incident to B with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
B |
A
|
True
|
0 |
False
|
|
B→C
|
B
|
C
|
False
|
4
|
True
|
|
E→B
|
B
|
E
|
False
|
0 |
False
|
Mark vertices C as visited, add it to the queue, set B as its parent, and add the edge to C.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| – | D |
–
|
–
|
(A→D, 3, 3) (C→D, 0, 1) (D→E, 01, 2) (D→F, 2, 6)
|
| – | E | – |
–
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 2, 6) (F→G, 2, 9)
|
| – | G | – |
–
|
(F→G, 2, 9) (E→G, 1, 1)
|
Dequeue C
|
C
|
Find edges incident to C with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
C→A
|
C
|
A
|
True | 3 | False |
|
B→C
|
C
|
B
|
True | 0 | False |
|
C→D
|
C
|
D
|
False | 1 | True |
|
C→E
|
C
|
E
|
False | 2 | True |
Mark vertices D and E as visited, add them to the queue, set C as their parent, and add the edges to D ad E.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| C | D | True |
(C→D, 0, 1)
|
(A→D, 3, 3) (C→D, 0, 1) (D→E, 1, 2) (D→F, 2, 6)
|
|
C
|
E | True |
(C→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 2, 6) (F→G, 2, 9)
|
| – | G | – |
–
|
(F→G, 2, 9) (E→G, 1, 1)
|
Dequeue D
| D |
E
|
Find edges incident to D with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→D
|
D
|
A
|
True
|
3 |
False
|
|
C→D
|
D
|
C
|
True
|
0 |
False
|
|
D→E
|
D
|
E
|
True
|
1 |
True
|
|
D→F
|
D
|
F
|
False
|
4 |
True
|
Mark vertices E and F as visited, add them to the Queue, set their parent to D, and add the edges.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| C | D | True |
(C→D, 0, 1)
|
(A→D, 3, 3) (C→D, 0, 1) (D→E, 1, 2) (D→F, 2, 6)
|
|
C
|
E | True |
(C→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| D | F | True |
(D→F, 2, 6)
|
(D→F, 2, 6) (F→G, 2, 9)
|
| – | G | – |
–
|
(F→G, 2, 9) (E→G, 1, 1)
|
Dequeue E
| E | F |
Find edges incident to E with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→B
|
E
|
B |
True
|
1 |
False
|
|
C→E
|
E
|
C |
True
|
0 |
False
|
|
D→E
|
E
|
D
|
True
|
1 |
False
|
|
E→G
|
E
|
G
|
False
|
0 |
False
|
Nothing to add since all adjacent vertices have been visited.
Dequeue F
| F |
Find edges incident to F with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
D→F
|
F
|
D
|
True
|
2 |
False
|
|
F→G
|
F
|
G
|
False | 7 | True |
Mark vertices G as visited, add it to the Queue, set its parent to F, and add the edge.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 0, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 0, 3)
|
(A→B, 0, 3) (B→C, 0, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 0, 4)
|
(C→A, 0, 3) (B→C, 0, 4) (C→D, 0, 1) (C→E, 0, 2)
|
| C | D | True |
(C→D, 0, 1)
|
(A→D, 3, 3) (C→D, 0, 1) (D→E, 1, 2) (D→F, 2, 6)
|
|
C
|
E | True |
(C→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| D | F | True |
(D→F, 2, 6)
|
(D→F, 2, 6) (F→G, 2, 9)
|
| F | G | True |
(F→G, 2, 9)
|
(F→G, 2, 9) (E→G, 1, 1)
|
Dequeue G
| G |
Find edges incident to G with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→G
|
G |
E
|
True
|
0 |
False
|
|
F→G
|
G |
F
|
True
|
2 |
False
|
Nothing to add.
HALT: Queue Empty
Determining the Path
Working backwards from G using the edgeTo array we determine the path to be: A, B, C, D, F, G
Determining the Bottleneck Capacity
Starting from the sink vertex G we work backwards to the source calculating the min residual capacity. The bottleneck is determined to be at edge
| Parent | To |
Back Edge
|
Capacity | Flow |
Max Flow
|
Bottleneck (min flow) |
New Flow
|
Edge To Before
|
Edge To After
|
| A | B |
False
|
3 | 0 | 3 | 1 | 1 |
(A→B, 0, 3)
|
(A→B, 1, 3)
|
| B | C |
False
|
4 | 0 | 4 | 1 | 1 |
(B→C, 0, 4)
|
(B→C, 1, 4)
|
| C | D |
False
|
1 | 0 | 1 | 1 | 1 |
(C→D, 0, 1)
|
(C→D, 1, 1)
|
|
D
|
F
|
False
|
6 |
2
|
4
|
1
|
3
|
(D→F, 2, 6)
|
(D→F, 3, 6)
|
|
F
|
G
|
False
|
9
|
2
|
7
|
1
|
3
|
(F→G, 2, 9)
|
(F→G, 3, 9)
|
Critical Edge = C→D
Max Flow = 1 + 2 + 1 = 4
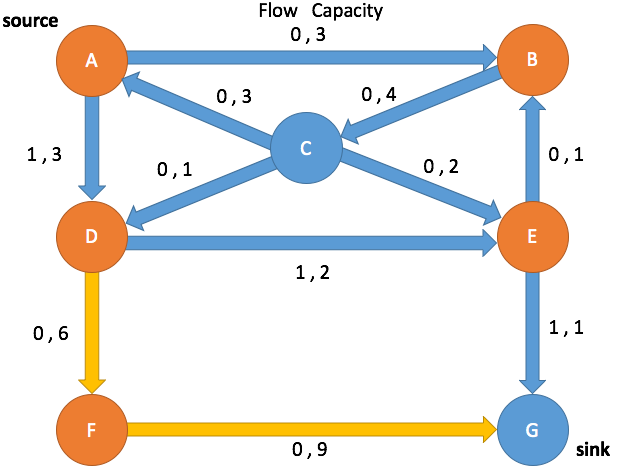
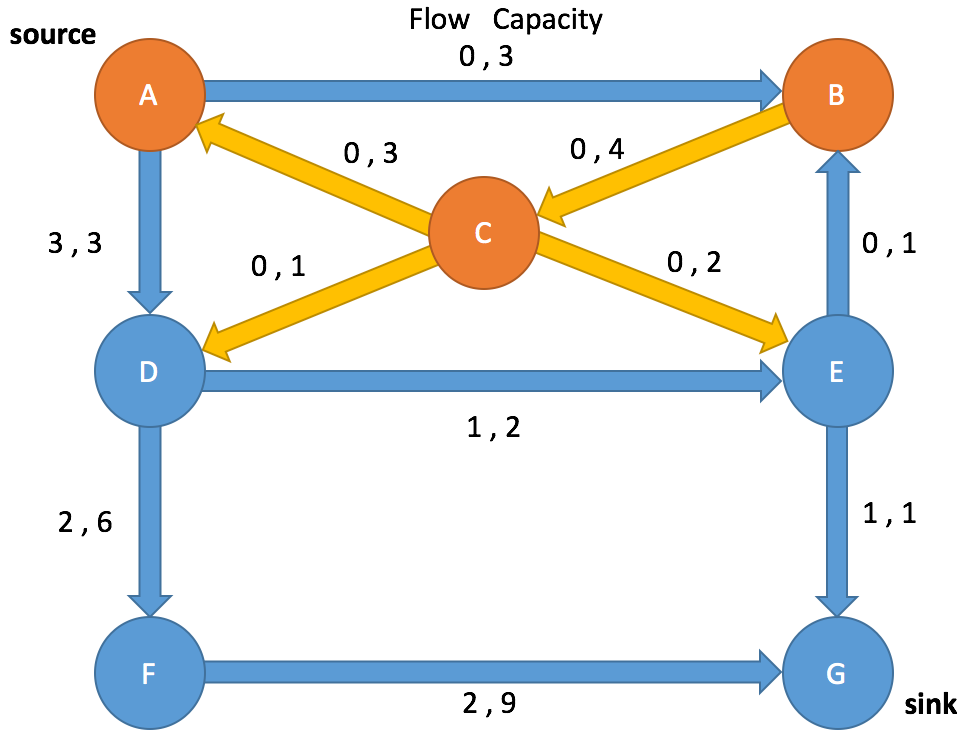
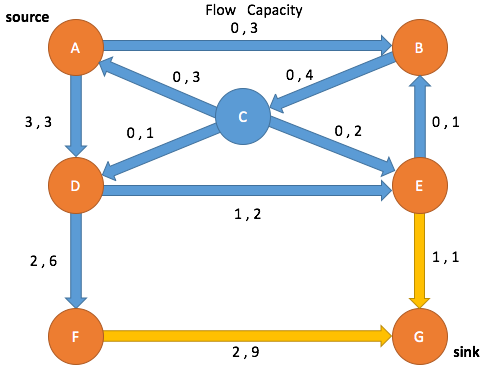
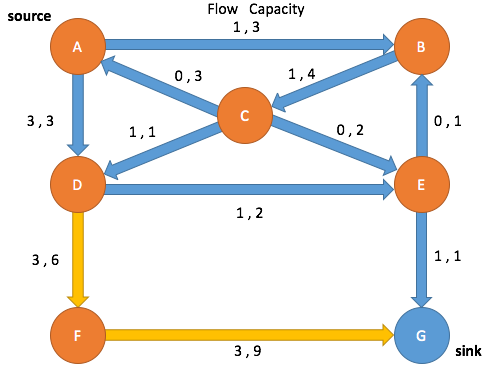
Path Search: Iteration 4
Enqueue A and mark as visited
|
A
|
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 1, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| – | B | – |
–
|
(A→B, 1, 3) (B→C, 1, 4) (E→B, 0, 1)
|
| – | C | – |
–
|
(C→A, 0, 3) (B→C, 1, 4) (C→D, 1, 1) (C→E, 0, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 1, 2) (D→F, 3, 6)
|
| – | E | – | – |
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 3, 6) (F→G, 3, 9)
|
| – | G | – |
–
|
(F→G, 3, 9) (E→G, 1, 1)
|
Dequeue A
|
A
|
Find edges incident to A with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
A
|
B
|
False
|
2 | True |
|
A→D
|
A
|
D
|
False
|
0 | False |
|
C→A
|
A
|
C
|
False
|
0 | False |
Mark vertices B as visited, add them to the queue, and add A as their parent, and add the edge to B.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 1, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 1, 3)
|
(A→B, 1, 3) (B→C, 1, 4) (E→B, 0, 1)
|
| – | C | – |
–
|
(C→A, 0, 3) (B→C, 1, 4) (C→D, 1, 1) (C→E, 0, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 1, 2) (D→F, 3, 6)
|
| – | E | – | – |
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 3, 6) (F→G, 3, 9)
|
| – | G | – |
–
|
(F→G, 3, 9) (E→G, 1, 1)
|
Dequeue B
|
B
|
Find edges incident to B with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
B |
A
|
True |
1
|
False
|
|
B→C
|
B
|
C
|
False | 3 | True |
|
E→B
|
B
|
E
|
False | 0 | False |
Mark vertices C as visited, add it to the queue, set B as its parent, and add the edge to C.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 1, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 1, 3)
|
(A→B, 1, 3) (B→C, 1, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 1, 4)
|
(C→A, 0, 3) (B→C, 1, 4) (C→D, 1, 1) (C→E, 0, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 1, 2) (D→F, 3, 6)
|
| – | E | – | – |
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 3, 6) (F→G, 3, 9)
|
| – | G | – |
–
|
(F→G, 3, 9) (E→G, 1, 1)
|
Dequeue C
|
C
|
Find edges incident to C with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
C→A
|
C
|
A
|
True
|
3
|
False
|
|
B→C
|
C
|
B
|
True |
1
|
False
|
|
C→D
|
C
|
D
|
False |
0
|
False
|
|
C→E
|
C
|
E
|
False |
2
|
True
|
Mark vertices E as visited, add it to the queue, set C as its parent, and add the edge to E.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 1, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 1, 3)
|
(A→B, 1, 3) (B→C, 1, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 1, 4)
|
(C→A, 0, 3) (B→C, 1, 4) (C→D, 1, 1) (C→E, 0, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 1, 2) (D→F, 3, 6)
|
| C | E | True |
(C→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 3, 6) (F→G, 3, 9)
|
| – | G | – |
–
|
(F→G, 3, 9) (E→G, 1, 1)
|
Dequeue E
| E |
Find edges incident to E with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→B
|
E
|
B |
True
|
1
|
False |
|
C→E
|
E
|
C |
True
|
0
|
False
|
|
D→E
|
E
|
D
|
False
|
1
|
True
|
|
E→G
|
E
|
G
|
False
|
0
|
False
|
Mark vertices D as visited, add it to the queue, set E as its parent, and add the edge to D.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 1, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 1, 3)
|
(A→B, 1, 3) (B→C, 1, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 1, 4)
|
(C→A, 0, 3) (B→C, 1, 4) (C→D, 1, 1) (C→E, 0, 2)
|
| E | D | True |
(D→E, 1, 2)
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 1, 2) (D→F, 3, 6)
|
| C | E | True |
(C→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 3, 6) (F→G, 3, 9)
|
| – | G | – |
–
|
(F→G, 3, 9) (E→G, 1, 1)
|
Dequeue D
| D |
Find edges incident to D with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→D
|
D
|
A
|
True
|
0
|
False
|
|
C→D
|
D
|
C
|
True
|
1 |
False
|
|
D→E
|
D
|
E
|
True
|
1
|
False
|
|
D→F
|
D
|
F
|
False
|
3
|
True
|
Mark vertices F as visited, add it to the Queue, set its parent to D, and add the edge.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 1, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 1, 3)
|
(A→B, 1, 3) (B→C, 1, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 1, 4)
|
(C→A, 0, 3) (B→C, 1, 4) (C→D, 1, 1) (C→E, 0, 2)
|
| E | D | True |
(D→E, 1, 2)
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 1, 2) (D→F, 3, 6)
|
| C | E | True |
(C→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| D | F | True |
(D→F, 3, 6)
|
(D→F, 3, 6) (F→G, 3, 9)
|
| – | G | – |
–
|
(F→G, 3, 9) (E→G, 1, 1)
|
Dequeue F
| F |
Find edges incident to F with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
D→F
|
F
|
D
|
True |
3
|
False
|
|
F→G
|
F
|
G
|
False
|
6
|
True
|
Mark vertices G as visited, add it to the Queue, set its parent to F, and add the edge.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 1, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 1, 3)
|
(A→B, 1, 3) (B→C, 1, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 1, 4)
|
(C→A, 0, 3) (B→C, 1, 4) (C→D, 1, 1) (C→E, 0, 2)
|
| E | D | True |
(D→E, 1, 2)
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 1, 2) (D→F, 3, 6)
|
| C | E | True |
(C→E, 0, 2)
|
(E→B, 0, 1) (C→E, 0, 2) (D→E, 1, 2) (E→G, 1, 1)
|
| D | F | True |
(D→F, 3, 6)
|
(D→F, 3, 6) (F→G, 3, 9)
|
| F | G | True |
(F→G, 3, 9)
|
(F→G, 3, 9) (E→G, 1, 1)
|
Dequeue G
| G |
Find edges incident to G with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→G
|
G
|
E |
True
|
1 | False |
|
F→G
|
G |
F
|
True
|
3
|
False
|
Nothing to add.
HALT: Queue Empty
Determining the Path
Working backwards from G using the edgeTo array we determine the path to be: A, B, C, E, D, F, G
Determining the Bottleneck Capacity
Starting from the sink vertex G we work backwards to the source calculating the min residual capacity. The bottleneck is determined to be at edge
| Parent | To |
Back Edge
|
Capacity | Flow |
Max Flow
|
Bottleneck (min flow) |
New Flow
|
Edge To Before
|
Edge To After
|
| A | B |
False
|
3 | 1 | 2 | 1 | 2 |
(A→B, 1, 3)
|
(A→B, 2, 3)
|
| B | C |
False
|
4 | 1 | 3 | 1 | 2 |
(B→C, 1, 4)
|
(B→C, 2, 4)
|
| C | E |
False
|
2 | 0 | 2 | 1 | 1 |
(C→E, 0, 2)
|
(C→E, 1, 2)
|
| E |
D
|
True
|
2 | 1 | 1 | 1 | 0 |
(D→E, 1, 2)
|
(D→E, 0, 2)
|
| D |
F
|
False
|
6 | 3 | 3 | 1 | 4 |
(D→F, 3, 6)
|
(D→F, 4, 6)
|
|
F
|
G |
False
|
9
|
3
|
6
|
1
|
4
|
(F→G, 3, 9)
|
(F→G, 4, 9)
|
Critical Edge = D→E
Max Flow = 1 + 2 + 1 + 1 = 5
Path Search: Iteration 5
Enqueue A and mark as visited
|
A
|
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 2, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| – | B | – |
–
|
(A→B, 2, 3) (B→C, 2, 4) (E→B, 0, 1)
|
| – | C | – |
–
|
(C→A, 0, 3) (B→C, 2, 4) (C→D, 1, 1) (C→E, 1, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 0, 2) (D→F, 4, 6)
|
| – | E | – |
–
|
(E→B, 0, 1) (C→E, 1, 2) (D→E, 0, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 4, 6) (F→G, 4, 9)
|
| – | G | – |
–
|
(F→G, 4, 9) (E→G, 1, 1)
|
Dequeue A
|
A
|
Find edges incident to A with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
A
|
B
|
False
|
1
|
True
|
|
A→D
|
A
|
D
|
False
|
0
|
False
|
|
C→A
|
A
|
C
|
False
|
0
|
False
|
Mark vertices B as visited, add them to the queue, and add A as their parent, and add the edge to B.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 2, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 2, 3)
|
(A→B, 2, 3) (B→C, 2, 4) (E→B, 0, 1)
|
| – | C | – |
–
|
(C→A, 0, 3) (B→C, 2, 4) (C→D, 1, 1) (C→E, 1, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 0, 2) (D→F, 4, 6)
|
| – | E | – |
–
|
(E→B, 0, 1) (C→E, 1, 2) (D→E, 0, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 4, 6) (F→G, 4, 9)
|
| – | G | – |
–
|
(F→G, 4, 9) (E→G, 1, 1)
|
Dequeue B
| B |
Find edges incident to B with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
A→B
|
B |
A
|
True |
2
|
False
|
|
B→C
|
B
|
C
|
False |
2
|
True |
|
E→B
|
B
|
E
|
Flase | 0 | False |
Mark vertices C as visited, add it to the queue, set B as its parent, and add the edge to C.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 2, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 2, 3)
|
(A→B, 2, 3) (B→C, 2, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 2, 4)
|
(C→A, 0, 3) (B→C, 2, 4) (C→D, 1, 1) (C→E, 1, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 0, 2) (D→F, 4, 6)
|
| – | E | – |
–
|
(E→B, 0, 1) (C→E, 1, 2) (D→E, 0, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 4, 6) (F→G, 4, 9)
|
| – | G | – |
–
|
(F→G, 4, 9) (E→G, 1, 1)
|
Dequeue C
| C |
Find edges incident to C with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to |
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
C→A
|
C
|
A
|
True | 3 | False |
|
B→C
|
C
|
B
|
True
|
2
|
False
|
|
C→D
|
C
|
D
|
False
|
0
|
False
|
|
C→E
|
C
|
E
|
False |
1
|
True |
Mark vertices E as visited, add it to the queue, set C as its parent, and add the edge to E.
Data Structures
|
Parent
|
To
|
Visited
|
Edge To |
Adjacent Edges (Edge, Flow, Capacity)
|
|
–
|
A | True |
–
|
(A→B, 2, 3) (A→D, 3, 3) (C→A, 0, 0)
|
| A | B | True |
(A→B, 2, 3)
|
(A→B, 2, 3) (B→C, 2, 4) (E→B, 0, 1)
|
| B | C | True |
(B→C, 2, 4)
|
(C→A, 0, 3) (B→C, 2, 4) (C→D, 1, 1) (C→E, 1, 2)
|
| – | D | – |
–
|
(A→D, 3, 3) (C→D, 1, 1) (D→E, 0, 2) (D→F, 4, 6)
|
| C | E | True |
(C→E, 1, 2)
|
(E→B, 0, 1) (C→E, 1, 2) (D→E, 0, 2) (E→G, 1, 1)
|
| – | F | – |
–
|
(D→F, 4, 6) (F→G, 4, 9)
|
| – | G | – |
–
|
(F→G, 4, 9) (E→G, 1, 1)
|
Dequeue E
| E |
Find edges incident to E with destination vertices that haven’t been visited, and that have residual capacities greater than zero.
Residual Capacity Calculations
|
edge
|
From
|
to
|
visited(to)
|
residualCapacity(to)
|
residualCapacity(to) > 0 && visited(Vertex) == False
|
|
E→B
|
E
|
B |
True
|
1
|
False
|
|
C→E
|
E
|
C |
True
|
1
|
False
|
|
D→E
|
E
|
D
|
False
|
0
|
False
|
|
E→G
|
E
|
G
|
False
|
0
|
False
|
Nothing to update.
HALT: Queue Empty
Max Flow Network
The algorithm halts with a calculated max flow of 5.
